|
Arithmetic Circuits, Real Numbers, and the Counting
Hierarchy
Eric Allender
Arithmetic circuit complexity is the object of intense study in
three different subareas of theoretical computer science:
- Derandomization. The problem of determining if two
arithmetic
circuits compute the same function is known as
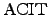 (arithmetic
circuit identity testing). (arithmetic
circuit identity testing). 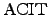 is the canonical example of a
problem in is the canonical example of a
problem in 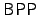 that is not known to have a deterministic
polynomial-time algorithm. Kabanets and Impagliazzo showed that the
question of whether or not that is not known to have a deterministic
polynomial-time algorithm. Kabanets and Impagliazzo showed that the
question of whether or not 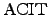 is in is in 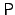 very tightly linked to
the question of proving circuit size lower bounds [5]. very tightly linked to
the question of proving circuit size lower bounds [5].
- Computation over the Reals. The Blum-Shub-Smale
model of
computation over the reals is an algebraic model that has received
wide attention [2].
- Valiant's Classes
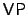 and and 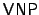 . Valiant characterized the
complexity of the permanent in two different ways. Viewed as a
function mapping . Valiant characterized the
complexity of the permanent in two different ways. Viewed as a
function mapping 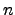 -bit strings to binary encodings of Natural
numbers, the permanent is complete for the class -bit strings to binary encodings of Natural
numbers, the permanent is complete for the class 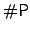 [7]. Viewed
as an n-variate polynomial, the permanent is complete for the class [7]. Viewed
as an n-variate polynomial, the permanent is complete for the class
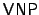 [6]. [6].
The general thrust of these three subareas has been in three
different directions, and the questions addressed seem quite
different from those addressed by work in the numerical analysis
community, such as that surveyed by Demmel and Koev [4].
This talk will survey some recent work that ties all of these
areas
together in surprising ways. Most of the results that will be
discussed can be found in [1,3], but I will also discuss some more
recent progress.
References
- [1]
- E. Allender,
P. Bürgisser, Johann Kjeldgaard-Pedersen, and
Peter Bro Miltersen. On the complexity of numerical analysis.
In
Proc. 21st Ann. IEEE Conf. on Computational Complexity (CCC
'06), pages 331-339, 2006.
- [2]
- L. Blum, F. Cucker,
M. Shub, and S. Smale. Complexity and
Real Computation. Springer, 1998.
- [3]
- P. Bürgisser. On defining
integers in the counting hierarchy and
proving lower bounds in algebraic complexity. Technical Report
TR06-113, Electronic Colloquium on Computational Complexity, 2006.
- [4]
- J. Demmel and P. Koev. Accurate
and efficient algorithms for
floating point computation. In Proceedings of the 2003
International Congress of Industrial
and Applied Mathematics, 2003.
- [5]
- V. Kabanets and R. Impagliazzo.
Derandomizing polynomial identity
tests means proving circuit lower
bounds. In Proc. ACM Symp. Theory Comp., pages 355-364, 2003.
- [6]
- L. Valiant. Completeness classes in
algebra. In Proc. ACM
Symp. Theory Comp., pages 249-261, 1979.
- [7]
- L. Valiant. The complexity of
computing the Permanent.
Theoret. Comp. Sci., 8:189-201, 1979.
An excursion through the algebras of  ukasiewicz
infinite-valued logic ukasiewicz
infinite-valued logic
Roberto Cignoli
J.  ukasiewicz introduced his systems of many-valued logics in
the early twenties of the last Century with a strong philosophical
motivation. MV-algebras were introduced by C. C. Chang in 1958
to give an algebraic proof of the completeness of certain axioms
for ukasiewicz introduced his systems of many-valued logics in
the early twenties of the last Century with a strong philosophical
motivation. MV-algebras were introduced by C. C. Chang in 1958
to give an algebraic proof of the completeness of certain axioms
for 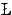 ukasiewicz infinite-valued logic. The aim of this talk is to
show some connections of MV-algebras with lattice-ordered
abelian groups, the Murray – von Neumann order of projections in
operator algebras, Ulam games with lies, toric varieties. ukasiewicz infinite-valued logic. The aim of this talk is to
show some connections of MV-algebras with lattice-ordered
abelian groups, the Murray – von Neumann order of projections in
operator algebras, Ulam games with lies, toric varieties.
Computably enumerable, strongly jump-traceable reals
Noam Greenberg
[slides]
Notions of traceability and lowness for randomness have been
intertwined since Terwijn and Zambella have shown that a real is low
for Schnorr tests iff it is computably traceable. Recently,
Figueira, Nies and Stephan introduced the class of strongly
jump-traceable reals. We show that in the computably enumerable
degrees, they form a proper sub-ideal of the 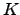 -trivial reals and
that none cup over -trivial reals and
that none cup over 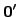 with a Martin-Löf random real.
Joint work with Rod Downey and Peter Cholak. with a Martin-Löf random real.
Joint work with Rod Downey and Peter Cholak.
Complexity and programming: the distinct meaning of one-way
functions in the continuous world
Joos Heintz
Joint work with B. Kuijpers, University of Hasselt, Belgium.
This talk is devoted to complexity issues in a simplified model
of
scientific computation (polynomial equation solving), taking into
account the interdependence of symbolic and numeric aspects.
Unlike in classic (bit) complexity theory, efficient encoding of
mathematical objects in scientific computing is often not
unique and the transition of one data structure to another
leads
generally to deep complexity problems of unknown status. Therefore
the corresponding computer programs should make use of rather
sophistic (higher type) data types (like circuits) and not only of
simple minded (type zero) data structures (like vectors and arrays).
This leads to a new model of (uniform) computation, which
includes specification, and correctness proofs by means of asserted
programs. The semantic and syntactic aspects of such computations
should be strongly separated.
Inspired by foundational questions of relational database
theory,
there exist already several attempts to model this situation by
means of a (hidden or explicit) concept of computing on structures
(see [1,2,3,5,12,13]). However these attempts do not reflect the
reality of programming and program execution, because they are based
on the implicit assumption of a unique encoding of the mathematical
objects under consideration. As a consequence of this hidden
assumption (e. g. of the isomorphism postulate of Y. Gurevich´s
Abstract State Machines [5]) one obtains a more or less immediate
proof that parametric geometric elimination requires
exponential sequential time.
On the other hand there exists an approach to complexity issues
with
non-unique data structures in a non-uniform model (based on
vectors and arrays of fixed length). In this context,
Constraint Database Theory is used in order to specify
algorithms.
This leads to the notion of geometric query. However, there
are elimination problems, which can be specified as geometric
queries and have intrinsically exponential complexity [8].
The Constraint Data Base model is also well suited in order to
characterize computational models, which are based on autonomous
calculations interleaved with querying inputs (frequently of higher
type) or environments (see [5,7,10,11]). As mentioned before, in
such models parametric geometric elimination requires
exponential sequential time.
Recursive algorithms with a priori bounded data swell (in the
spirit
of the Bellantoni- Cook characterization [4,7] of the class P) are
not expressive enough for elimination tasks. On the other hand, the
recursive call of even optimal elimination algorithms leads to
uncontrolled data swell. In order to circumvent this difficulty,
recursive elimination algorithms have to reduce stepwise their
intermediate results to intrinsic geometric data. However it may
happen that the expansion of such a reduced intermediate result may
become of intrinsic exponential complexity, at least if one requires
that the algorithm remains "numerically robust" [6].
Such an instance is given by the robust numerical interpolation
of
polynomial functions with low approximative arithmetic circuit
complexity [9].
This example shows also a substantial difference between
discrete
and continuous computing: whereas the existence and the exhibition
of one-way functions is a fundamental problem in discrete
computation with many application, a formal translation of the same
question to the continuous world is not too difficult to answer
[6,9].
References
- [1]
- S. Abiteboul, C. H.
Papadimitriou, V. Vianu. The Power of
Reflective Relational Machines. Logic in Computer Science (1994)
230-240
- [2]
- S. Abiteboul, C. H. Papadimitriou, V.
Vianu . Reflective
Relational Machines. Information and Computation, 143 (2) (1998)
110-136
- [3]
- S. Abiteboul, V. Vianu. Computing on
Structures. In Proceedings
of the 20th international Colloquium on Automata, Languages and
Programming. A. Lingas, R. G. Karlsson, and S. Carlsson, Eds.
Springer LNCS 700 (1993) 606-620
- [4]
- S. Bellantoni, S. Cook. A new
recursion-theoretic
characterization of the polytime functions. Comput. Complex. 2 (2)
(1992) 97-110
- [5]
- A. Blass, Y. Gurevich. Ordinary
interactive small-step
algorithms, I. ACM Trans. Comput. Logic 7 (2) (2006), 363-419
- [6]
- D. Castro, M. Giusti, J. Heintz, G.
Matera, L. M. Pardo. The
hardness of polynomial equation solving. Foundations of
Computational Mathematics 3 (2003) 1-74
- [7]
- P. Clote. Computational Models and
Function Algebras. In
Selected Papers From the international Workshop on Logical and
Computational Complexity. D. Leivant, Ed. Springer LNCS 960 (1994)
98-130.
- [8]
- M. Giusti, J. Heintz, B. Kuijpers. The
evaluation of geometric
queries: constraint databases and quantifier Elimination. Manuscript
Hasselt University (2006)
- [9]
- J. Heintz, B. Kuijpers. Constraint data
bases, data structures
and efficient query elimination. Constraint Databases. Proceedings
of the 1st International Symposium Applications of Constraint
Databases (CDB'04), B. Kuijpers, P. Revesz, eds., Springer LNCS 3074
(2004) 1-24.
- [10]
- B. Kapron, S. A. Cook. A new
characterization of Mehlhorn's
polynomial time functionals. 32nd Annual Symposium on Foundations of
Computer Science (1991) 342-347
- [11]
- K. Mehlhorn. Polynomial and abstract
subrecursive classes.
Proceedings of the Sixth Annual ACM Symposium on theory of Computing
STOC '74. ACM Press (1974) 96-109
- [12]
- Y. Moschovakis. What Is an Algorithm?
Björn Engquist and
Wilfried Schmid, Eds. Mathematics Unlimited - 2001 and Beyond.
Springer Verlag (2001)
- [13]
- Y. Moschovakis. On founding the theory
of algorithms. Truth in
mathematics H. G. Dales and G. Oliveri, Eds., Clarendon Press,
Oxford (1998) 71-104.
Countable
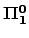 classes, strong degree spectra,
and Kolmogorov complexity classes, strong degree spectra,
and Kolmogorov complexity
Carl G. Jockusch
[slides]
This is joint work with John Chisholm, Jennifer Chubb, Valentina
Harizanov, Denis Hirschfeldt, Timothy McNicholl, and Sarah Pingrey.
We study the weak truth-table spectra of relations on computable
models. A basic result is that 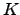 is not wtt-reducible to the is not wtt-reducible to the
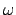 -part of any computable linear ordering of order-type -part of any computable linear ordering of order-type
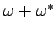 . Further, we show that there is a low c.e. set . Further, we show that there is a low c.e. set
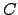 which is not wtt-reducible to any element of any countable which is not wtt-reducible to any element of any countable
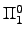 subset of subset of 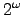 , and hence is not wtt-reducible to
any initial segment of any scattered computable linear order.
Kolmogorov complexity is used to greatly simplify the original
proof of this result. , and hence is not wtt-reducible to
any initial segment of any scattered computable linear order.
Kolmogorov complexity is used to greatly simplify the original
proof of this result.
Low upper bounds of ideals
Antonin Kucera
[slides]
This is a joint project with T. Slaman.
We show that there is a low upper bound for the class 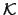 ,
i.e. the class of ,
i.e. the class of 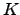 -trivial sets. The result can be strengthened
to a more general characterization of ideals of r.e. sets for which
there is a low upper bound. Coding into -trivial sets. The result can be strengthened
to a more general characterization of ideals of r.e. sets for which
there is a low upper bound. Coding into 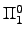 -classes plays an
important role here, as well as in some other applications. -classes plays an
important role here, as well as in some other applications.
Dimensions of points on lines and curves
Steffen Lempp
This is a joint work with Jack Lutz. I will present recent new
results on the (constructive Hausdorff) dimensions of individual
points on lines and curves in Euclidean space.
Traceability and Kolmogorov complexity
Wolfgang Merkle
We review known and recent results about the relations between
variants of traceability and concepts defined in terms of
Kolmogorov complexity such as autoreducibility or lowness for
Kolmogorov complexity.
Randomness, Lowness Notions, Measure and Domination
Joseph S. Miller
[slides]
An oracle 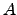 is low for a given computability theoretic class if
relativizing to is low for a given computability theoretic class if
relativizing to 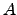 does not change the class. The oracles that are
low for Martin-Löf randomness are a particularly interesting
example. They were introduced by Zambella in 1990 and several
characterizations were given in papers of Nies, Hirschfeldt, Stephan
and others. Recently, Downey, Nies, Weber and Yu proved that every
oracle low for weak does not change the class. The oracles that are
low for Martin-Löf randomness are a particularly interesting
example. They were introduced by Zambella in 1990 and several
characterizations were given in papers of Nies, Hirschfeldt, Stephan
and others. Recently, Downey, Nies, Weber and Yu proved that every
oracle low for weak 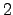 -randomness is low for ML-randomness. We see
that the reverse is also true.
This work is related to two domination properties introduced by
Dobrinen and Simpson: almost everywhere domination and its uniform
variant. Following up on work of Kjos-Hanssen, we explain how
lowness properties relate to measure regularity properties and thus
to domination properties. We can use this relationship to prove that
the domination properties of Dobrinen and Simpson are equivalent. -randomness is low for ML-randomness. We see
that the reverse is also true.
This work is related to two domination properties introduced by
Dobrinen and Simpson: almost everywhere domination and its uniform
variant. Following up on work of Kjos-Hanssen, we explain how
lowness properties relate to measure regularity properties and thus
to domination properties. We can use this relationship to prove that
the domination properties of Dobrinen and Simpson are equivalent.
Profinite topologies on words
Jean-Éric Pin
[slides]
Profinite topologies were introduced by M. Hall Jr, originally
for
the free group. Over the past twenty years, they found surprising
applications in the theory of finite automata. In this survey
lecture, I shall introduce the main definitions, give several
examples and present some of the main results of this theory.
Effectively closed sets of measures and randomness
Jan Reimann
[slides]
We study effectively closed sets of measures under the weak
topology. These have been used by Levin to prove results on the
existence of uniform tests of randomness or neutral measures. We
show how to use standard techniques concerning 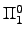 classes,
such as basis theorems, to obtain results concerning the relation
between randomness for Hausdorff and probability measures, as well
as give new, information theoretic proofs of fundamental results in
geometric measure theory. classes,
such as basis theorems, to obtain results concerning the relation
between randomness for Hausdorff and probability measures, as well
as give new, information theoretic proofs of fundamental results in
geometric measure theory.
Pseudorandom generators, a survey
Claus-Peter Schnorr
[slides]
Pseudorandom numbers play an important role in many modern
applications. In particular, public and private key cryptographic
schemes use pseudorandom numbers for encryption, authentication and
digital signatures. The corresponding pseudorandom number generation
must be both efficient and provably secure.
We survey highlights of the development of pseudorandom
generators
since their invention due to Yao and Blum-Micali in 1982. We focus
on practical generators that are provably secure under reasonable
complexity assumptions such as the complexity of integer
factorization, the complexity of the discrete logarithm and the
complexity of lattice problems.
While the hardness of factoring integers gives rise to the
elegant
modular squaring generator of Blum-Blum-Shub the discrete logarithm
problem has the advantage of being harder, in particular for generic
groups like elliptic curves. However, if quantum computers can be
build the complexity of factoring and of the discrete logarithm
break down. For this case it seems best to construct pseudorandom
generators based on NP-hard problems. NP-hard lattice problems are
particular appropriate.
The theories of Turing degree structures
Richard A. Shore
This talk will primarily be an exposition of the general
approaches
to proving that the theories of various Turing degree structures are
undecidable or even as complicated as full first or second order
arithmetic. The methods that we shall consider are all, from a
methodological point of view, ones proceeding by the interpretation
of some standard theory such as that of partial orderings or a
finitely axiomatized version of arithmetic. For each structure
considered, specific methods and set constructions will be described
that implement the desired interpretations. We will consider the
structures 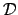 , the Turing degrees of all sets; , the Turing degrees of all sets;
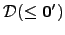 , the Turing degrees of the
sets computable from the Halting problem; and , the Turing degrees of the
sets computable from the Halting problem; and 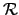 , the
Turing degrees of the recursively enumerable sets. We also expect to
describe some new joint work with Ted Slaman giving results along
these
lines for the structures , the
Turing degrees of the recursively enumerable sets. We also expect to
describe some new joint work with Ted Slaman giving results along
these
lines for the structures
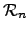 , the Turing degrees of the , the Turing degrees of the 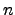 -r.e. sets.
Note: There is a common framework in which one can define the
three
proper substructures of -r.e. sets.
Note: There is a common framework in which one can define the
three
proper substructures of 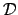 that we will consider. We say
that that we will consider. We say
that 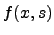 is an approximation to a set
is an approximation to a set 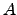 if for every if for every 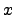 , , 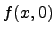 , ,
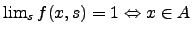 and and
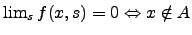 . By definition, for each . By definition, for each
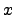 , the set , the set
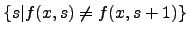 of stages at which an
approximation of stages at which an
approximation 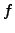 changes its value at changes its value at 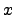 is finite. In this
setting, we note that is finite. In this
setting, we note that 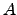 is computable from is computable from 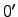 if and
only if it has a recursive approximation. if and
only if it has a recursive approximation. 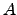 is r.e. if and only if
it has a recursive approximation that, for each is r.e. if and only if
it has a recursive approximation that, for each 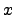 , changes its
value at , changes its
value at 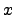 at most once. at most once. 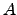 is is 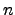 -r.e. if and only if it has a
recursive approximation that, for each -r.e. if and only if it has a
recursive approximation that, for each 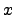 , changes its value at , changes its value at 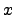 at most
at most 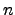 many times. many times.
Moduli of computation
Theodore Slaman
[slides]
In this talk, we will discuss joint work with Marcia Groszek,
Dartmouth College, in which we examine sets recursive in all
sufficiently-quickly growing functions. We say that
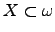 has a modulus (of computation) has a modulus (of computation)
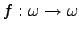 if and only if every function
if and only if every function 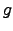 which dominates which dominates 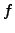 pointwise
computes pointwise
computes 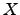 . If . If 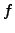 is recursive in is recursive in 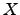 , then we say that , then we say that 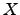 has
a self-modulus.
By a theorem of Solovay, every set which has a modulus is has
a self-modulus.
By a theorem of Solovay, every set which has a modulus is
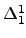 . We show that if . We show that if 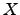 has a self-modulus then either has a self-modulus then either
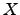 is is 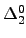 or or 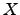 computes a 1-generic. We give examples
to show that these cases are nondegenerate. In particular, there is
a nonrecursive set computes a 1-generic. We give examples
to show that these cases are nondegenerate. In particular, there is
a nonrecursive set 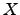 with a self-modulus which does not compute
any nonrecursive with a self-modulus which does not compute
any nonrecursive 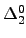 set.
Other connections between rates of growth and genericity will be
discussed as time allows. set.
Other connections between rates of growth and genericity will be
discussed as time allows.
Incomputability in games, wars and economics -
Inductive
inference in hostile environments
Ray Solomonoff
We know that the very best probability evaluation functions are
incomputable. We also know that for any computable approximation to
such functions, there exist hostile environments in which this
approximation is catastrophically bad.
One way of dealing with environments of this sort is to have
larger
computation resources than the hostile environment and/or use our
resources more efficiently. We will consider the problem of getting
the very best probability estimates using whatever resources we
happen to have.
For resource bounds of this kind, a variant of Levin's Search
Procedure is able to give near optimum predictions - but with
certain restrictions. We will examine these restrictions and
propose techniques to transcend them.
Intervals in the Medvedev lattice
Sebastiaan A. Terwijn
The Medvedev lattice is a structure from computability theory
with
ties to constructive logic. We will briefly describe this connection
and the relation to structures such as the Turing degrees. We will
then discuss structural properties of the Medvedev lattice, in
particular, the size of its intervals. We prove that every interval
in the lattice is either finite, in which case it is isomorphic to a
finite Boolean algebra, or contains an antichain of size
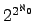 , the size of the lattice itself. We also prove
that it is consistent that the lattice has chains of this size, and
in fact that these big chains occur in every interval that has a big
antichain. We also study embeddings of lattices and algebras. We
show that large Boolean algebras can be embedded into the Medvedev
lattice as upper semilattices, but that a Boolean algebra can be
embedded as a lattice only if it is countable. Finally we discuss
which of these results hold for the closely related Muchnik lattice. , the size of the lattice itself. We also prove
that it is consistent that the lattice has chains of this size, and
in fact that these big chains occur in every interval that has a big
antichain. We also study embeddings of lattices and algebras. We
show that large Boolean algebras can be embedded into the Medvedev
lattice as upper semilattices, but that a Boolean algebra can be
embedded as a lattice only if it is countable. Finally we discuss
which of these results hold for the closely related Muchnik lattice.
Genericity theory from the randomness
Liang Yu
[slides]
I shall survey recent results about genericity in the light of
randomness theory. It is well known that there are many analogies
between category and measure theory. So it is natural compare
genericity theory with randomness theory. In particular, we focus on
the lowness properties for genericity and obtain a complete
description. We also compare n-genericity with n-randomness in the
both recursion theory and set theory aspects.
|





